GLNF Loge : Lou Prieurat de Sant-Peire - Orient de La Garde  Date : NC

Le Nombre d'Or

C’est au début du XXe siècle que la lettre grecque PHI- initiale de Phidias (sculpteur grec) - fut proposée pour désigner le nombre d'or.
L'ubiquité de (phi) en mathématique avait éveillé l'intérêt de nombreux mathématiciens au Moyen Age et à la Renaissance.
L'apparition du nombre d'or remonte à la préhistoire.
Ayant appris à diviser un cercle en 5 ou en 10, les hommes en vinrent au pentagone et au décagone, et dès lors ils avaient sous les yeux le nombre d'or.
Ce sont aux Grecs que l'on doit la science de la géométrie, mais c'est à Euclide que l'on est redevable d'un véritable traité écrit.
Ce nombre noté phi est la racine positive de l'équation x²-x-1=0. Il vaut donc environ 1,618.    

Il revient à la mode à la Renaissance.
En 1509, Luca Pacioli publie un ouvrage intitulé « Divina Proportione » , illustré par Léonard de Vinci : premier traité consacré pour une large part au nombre d'or.
L'époque contemporaine fait une large place au nombre d'or, en particulier avec le peintre Sérusier et l'architecte Le Corbusier.
7033-4-1

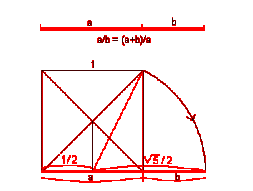
7033-4-2
Euclide (3 siècles avant JC ) est célèbre pour son traité de géométrie : Les Éléments.
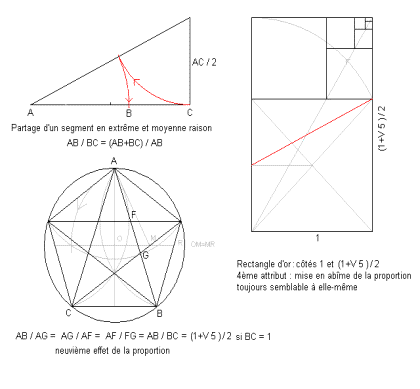
Il a donné les propriétés des pentagones et des décagones réguliers.
Nous trouvons déjà dans son œuvre une théorie des proportions et en particulier le partage d'un segment en moyenne et extrême raison.
Cela signifie que l'on cherche le point  du segment tel que: la longueur totale a+b rapportée à la longueur du grand segment a est dans la même proportion que celle du grand segment a par rapport au petit segment b. 
Ce segment est partagé suivant la section d'or ou la proportion divine

Les rapports (a+b)/a et a/b étant égaux, de l'équation   a / b = ( a + b ) / a
on ontient l'équation ( a / b )² - a / b - 1 = 0

C

B

A
dont la solution est : a / b =  j ou nombre d'or

7033-4-3

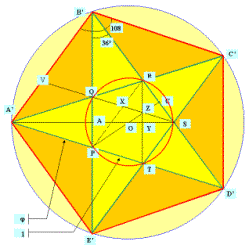
Toutes ces figures sont liées au nombre d'or et génèrent des suites de dessins semblables au dessin initial.

1. Le pentagramme

On pense que c'était le signe de ralliement des Pythagoriciens. Le pentagramme était considéré par les anciens comme un symbole universel de perfection et de beauté. On le retrouve dans des créations artistiques, sur certaines monnaies, dans les rosaces des cathédrales, sur des drapeaux

7033-4-4

2. Triangles d'or   
Ce sont des triangles dont le rapport des longueurs des côtés est phi. 
Il y en a deux : un à angle obtus, l’autre à angle aigu.  
7033-4-5
Le pentagone est l’union de trois triangles d’or
Si l'on prend le triangle suivant et que l'on coupe ce triangle par une bissectrice, on obtient 2 nouveaux triangles : ce sont encore des triangles d'or.
Ce processus peut se répéter, les triangles deviennent de plus en plus petit et semblent s'enrouler autour d'un point limite.
Ce point est à l'intersection des médianes des triangles successifs créés par la divisons.

7033-4-6

Le pentagone est l’union de trois triangles d’or
Si l'on prend le triangle suivant et que l'on coupe ce triangle par une bissectrice, on obtient 2 nouveaux triangles : ce sont encore des triangles d'or.
Ce processus peut se répéter, les triangles deviennent de plus en plus petit et semblent s'enrouler autour d'un point limite.
Ce point est à l'intersection des médianes des triangles successifs créés par la divisons.

3. Le pentagone          

7033-4-4

Deux propriétés :
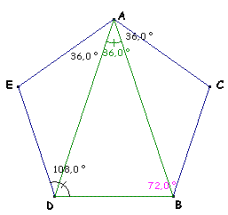
Le côté du pentagone étoilé est phi fois le côté du pentagone convexe.  
Chacun des 5 côtés partage 2 autres côtés selon le nombre d'or.

Située sur la commune de Crots dans une forêt domaniale, entre Embrun et le lac de Serre-Ponçon, l'abbaye de Boscodon organise des visites, ou sorte de séminaires,  avec des thèmes adaptés à l’age des visiteurs, sous forme de cahier : les cahiers de Boscodon.
Ces cahiers sont un moyen simple d’apprendre le tracé de formes géométriques où le nombre d’or est omniprésent, s’appuyant sur des exemples réels tels que plans de cathédrales, d’abbayes, études de tableau et curiosités de la nature.
L’utilisation de compas, équerre, niveau, corde à douze nœuds…. y est décrite avec simplicité, et permet par la suite, de regarder sous un autre angle, le fruit des bâtisseurs.

Le nombre d’or et les mathématiques :

7033-4-7

 7033-4-8

Léonard de Pise, plus connu sous le nom de Fibonacci , est né à Pise vers 1180 et mort vers 1250.

Le problème de son livre qui a le plus inspiré les mathématiciens est le problème des lapins : "Combien de couples de lapins obtiendrons-nous à la fin de chaque mois si commençant avec un couple, chaque couple produit chaque mois un nouveau couple, lequel devient productif au second mois de son existence."

Ce problème donne lieu à la suite de FIBONACCI :
1 ; 1 ; 2 ; 3 ; 5 ; 8 ; 13 ; 21 ; 34 ; 55 ; 89 ; 144 ; 233 ; 377 ;....
Chaque terme est la somme des deux termes qui le précèdent .

PROPRIÉTÉS DE LA SUITE DE FIBONACCI :
Le rapport des termes consécutifs se rapproche du nombre d'or phi=1,618033989 .
2/1=2 ;  3/2=1,5 ;  5/3=1,666 ;  8/5=1,6 ; 13/8=1,625; 21/13=1,615;  34/21=1,619 ; 55/34=1,617 ; 89/55=1,6181818....   144/89=1,617977..     233/144=1,61805...

7033-4-9

Une dernière illustration montrant une figure géométrique générée par le nombre d’or, représentée par un tableau de Pierre WITTMANN de 1989.
Partant du centre, une ligne coupera plusieurs la spirale, chaque distance séparant les intersection sous successivement dans le rapport du nombre d’or.
Le Nombre d'Or correspond à une proportion particulièrement harmonieuse . Elle se retrouve dans de nombreux monuments, peintures, et dans la nature.

Le nombre d’or et l’architecture :

Au moyen âge, les bâtisseurs de cathédrales utilisaient une pige constituée de cinq tiges articulées, correspondant chacune à une unité de mesure de l'époque, relative au corps humain : la paume, la palme, l'empan, le pied et la coudée.

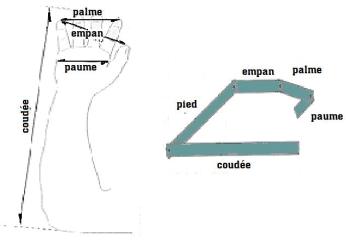
7033-4-A

Les longueurs étaient donnée en lignes, une ligne mesurant environ 2 mm (précisément 2,247 mm) :

7033-4-B
Pour passer d'une mesure à la suivante, on peut constater que l'on multiplie par le nombre d'or , environ 1,618.
Une illustration pour mieux comprendre le rapport entre chaque unité de mesure

7033-4-C

Le Corbusier et le Modulor

7033-4-D

Le Corbusier (1887-1965) est un architecte français d'origine Suisse.
Il  s'inspire de l'esthétique fonctionnelle des machines, propose le recours à des formes de plans verticaux, adopte le principe de forme géométrique simple.
Il cherche à appliquer le Modulor (système de proportion).
Il a tendance à accentuer le caractère plastique des formes.

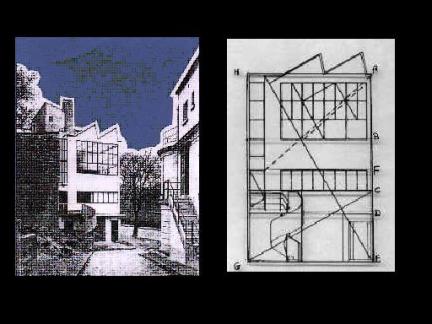
7033-4-E

Dans son étude de la Maison :

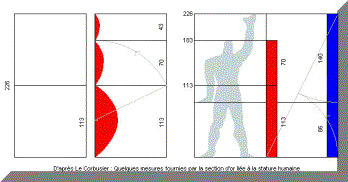
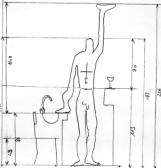
On constate que la balustrade, le rebord en ciment, les fenêtres du premier et deuxième étage sont placés selon le rapport phi. De plus, la façade s'inscrit à peu prés dans un rectangle d'or.

Le Modulor est une application du nombre d’or qui met en évidence la relation des différentes grandeurs du corps humain entre elles.

7033-4-F

7033-4-G
De cette application au corps humain, il en découle   différentes hauteurs de mobiliers, d’aménagements du cadre de vie de l’homme aux belles proportions.
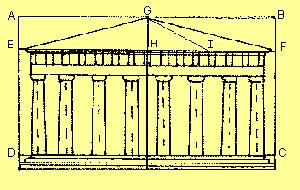
Le parthénon

 7033-4-H

 7033-4-I

Le Parthénon d'Athènes fait apparaître un peu partout le nombre d'or .
Certains se sont employés à le chercher et l'ont bien sûr trouvé !

Le Parthénon s'inscrit dans un rectangle doré, c'est-à-dire tel que le rapport de la longueur à la hauteur était égal au nombre d'or.

La grande pyramide de Khéops

7033-4-J

Il paraît que ...
Le rapport de la hauteur de la pyramide de Khéops par sa demi-base est le nombre d'or.
D'après Hérodote, des prêtres égyptiens disaient que les dimensions de la grande pyramide avaient été choisies telles que : "Le carré construit sur la hauteur verticale égalait exactement la surface de chacune des faces triangulaires.

Le nombre d’or et la peinture

Ce rapport fut baptisé "Divine Proportion" par le moine Fra Luca Pacioli (1445 - 1517 Rome) qui lui consacra le traité Divina Proportione, illustré par Léonard de Vinci (1452-1519)

7033-4-K

Ce tableau, de Jicopo de Barbari, où Fra Luca Pacioli explique un théorème, fait apparaitre le partage " en extrème et moyenne raison " (la " divine proportion ").
On y retrouve en effet, le nombre d'or : la projection orthogonale de l'extrémité de l'index de la main gauche du moine divise le tableau selon la section dorée, ainsi que le pouce et l'index gauches de Fra Luca Pacioli partage la hauteur du livre selon le même rapport. 

Léonard De Vinci a donc illustré l’ouvrage de Luca Pacioli en 1558 dans son traité sur les polyèdres réguliers

 7033-4-M

 7033-4-L

 7033-4-N
De son étude sur ces polyèdres, on observera l’ icosaèdre qui est un polyèdre limité par vingt faces. L'icosaèdre est régulier quand ses faces sont des triangles équilatéraux égaux entre eux. Il est inscriptible dans une sphère par ses douze sommets.
Ils se situent aux angles de trois rectangles d'or qui sont en position symétrique les uns par rapport aux autres, mutuellement perpendiculaires, leur point commun étant le centre de l'icosaèdre.

On ne peux parler de Léonard de Vinci sans citer son illustration de l’Homme de Vitruve, où, reprenant les proportions idéales de l’homme données par Vitruvius Pollio, architecte, natif de Vérone, du 1er s. av. J., de Vinci l’inscrit dans un cercle parfait, ainsi que dans un carré, le nombril au centre du cercle, divisant son corps dans le rapport du nombre d’or.
Par le symbole du cercle et du carré, cette illustration situe l’homme  comme intermédiaire entre le ciel et la terre, comme lien entre l’immatériel et le matériel.

La Naissance de Vénus de Botticelli
Une étude graphique à mis en évidence les proportions du nombre d’or dans le tableau

7033-4-O

De même dans ce tableau de la vierge à l’enfant de Raphael, cercle et triangles d’or ont bien servis de trame au peintre.

7033-4-P

Finalement, soulignons qu'un artiste voulant mettre en oeuvre la section d'or dans ces tableaux doit y rattacher clairement les éléments majeurs de ses compositions. Cela signifie que la section d'or permettra à l'artiste de mettre l'emphase sur les éléments importants de son œuvre, sur ce qui doit davantage attirer l'attention du spectateur.

Le nombre d’or et la musique

7033-4-Q

Beaucoup d'auteurs vantent la beauté de la forme du violon.
Une forme est belle lorsque les rapports entre ses diverses dimensions respectent un certain nombre de lois géométriques et perspectives.
A l'époque de la création du violon, l'esthétique des proportions préoccupait nombre d'artistes
Plusieurs chercheurs ont tenté l'analyse de la forme du violon à l'aide du nombre d'or, et l'on a même retrouvé des coïncidences qu'on peut difficilement attribuer au hasard .

Un des mystères de l'oeuvre monumentale de Jean-Sébastien Bach est éclairci: le musicien allemand appliquait la règle du nombre d'or à ses compositions.
Par une analyse méticuleuse de la fugue de la Suite en do mineur pour luth, Guy Marchand, découvreur du secret, en a fait ressortir la construction symétrique inusitée. «Cette fugue est exceptionnelle par sa construction, car il y a tout un jeu de retours périodiques. Les épisodes et les sujets sont traités de façon récurrente», note-t-il.
La petite fugue de la Suite en do mineur de Jean-Sébastien Bach est construite d'après les mesures du nombre d'or établies par le mathématicien italien Fibonacci. En analysant la fugue, Guy Marchand a confirmé l'utilisation du nombre d'or par Bach au 17e siècle.
Fervent chrétien, Bach a appliqué les thèses de Martin Luther à sa musique, faisant de son oeuvre un hommage à la gloire de Dieu. Ainsi, la Suite en do mineur dépeint la difficile expérience des hommes et la pratique de leur foi chrétienne. La construction harmonique en chutes correspond à l'égarement des hommes sous l'emprise de Satan. Enfin, l'ascension finale représente le salut des âmes par Dieu.

Le nombre d’or dans la nature

Lorsque nous regardons attentivement certains végétaux, on peut y découvrir le nombre d'or. Cependant, c'est depuis peu que nous avons compris pourquoi chez de nombreux végétaux, feuilles, écailles et pétales forment des spirales qui sont reliées au nombre d'or. Ces figures ne font pas parties du patrimoine génétique de ces végétaux, mais plutôt de leur dynamique de croissance qui provoque l'apparition de ces spirales liées au nombre d'or. En effet, lors de la croissance de ces végétaux, on remarque la constance du nombre d'or. Par exemple, dans la pomme de pin, on retrouve 5 spirales dans le sens des aiguilles d'une montre et 8 dans le sens opposé, ou 8 et 13 chez l'ananas ou même 34 et 58 pour le tournesol

7033-4-R

Nous retrouvons encore les nombres appartenant à la suite de Fibonaci

 7033-4-S

 7033-4-T.jpg

Le règne animal n‘est pas de reste pour nous rappeler  pentagrammes et autres spirales dorées…

La « proportion dorée » est bien connue, dans la Bible, en tant que rapport 3/5 (ou 30/50 ou 1,5 / 2,5). Qu’on en juge :

• L’Arche de Noé
Cette arche, tu la feras longue de 300 coudées, large de 50 et haute de 30
Genèse 6,15

Nous voyons ici, entre la largeur (50) et la hauteur (30), la proportion 30/50, c’est à dire 0,6. Quant à la longueur (300), elle est triple de la construction suivante :

• La maison de Salomon
La maison que le roi Salomon se fait bâtir (la maison des cèdres) est exactement le tiers de l’Arche de Noé :
Elle avait 100 coudées de longueur, 50 coudées de largeur et 30 coudées de hauteur
I Rois 7,2

Dans les deux cas, largeur et hauteur sont dans la même « proportion dorée ».
C’est encore le cas dans les exemples suivants :

• L’autel des sacrifices 
Tu feras l’autel en bois d’acacia : 5 coudées de long, 5 coudées de large -l’autel sera carré- et 3 coudées de haut
Exode 27,1

Le côté du carré est en proportion dorée de la hauteur de l’autel.

•  Il est encore d’autres exemples, mais ce qui précède est sans doute suffisant. Les constructions répondent à une intention symbolique précise -tout comme les constructeurs des églises médiévales obéissent à des normes jugées significatives. De ce point de vue, l’Écriture (spécialement le Pentateuque (ensemble formé par les cinq premiers livres de la Bible ; les Juifs le nomme ''Torah'')) est un grand temple où les formes sont porteuses de signification.

Ce n’est pas le nombre isolé qui est ici porteur de signifiance, mais la proportion indiquée. Il serait naïf de penser que ces proportions ont été indiquées au hasard par des scribes ignorants. Et les études qui ne tiennent pas compte de ce symbolisme sont superficielles -éventuellement savantes, mais superficielles.

L’utilisation symbolique des nombres a été très développée dans les textes bibliques. Deux raisons à cela : d’une part, tout ce qui existe, dans le ciel et sur la terre, lois physiques ou lois religieuses, nombres ou figures…. proviennent d’un unique créateur. Les nombres sont le miroir de cette origine. D’autre part, les nombres sont abstraits et leur utilisation ne viole en rien l’interdiction de se faire des représentations de ce qui est là-haut dans le ciel ou ici-bas sur la terre. Ce sont des symboles, non des images. Des supports de compréhension, non des représentations à adorer.

De là, l’utilisation d’un symbolisme numérique dans la mise en forme de nombreux textes bibliques. De sorte que beaucoup de textes peuvent être lus « simplement », selon une construction narrative, législative ou poétique « ordinaires ». Mais une autre lecture, symbolique, est possible -ce qui demande une longue initiation…

La divine proportion est donc omniprésente, sous nos yeux.

La nature l’utilisant pour des besoins de vie, de croissance, une règle d’évolution bien moins rapide que l’exponentialité et plus douce que la multiplicité cellulaire qui ne sait que diviser pour mieux se multiplier.

L’homme, dans ses créations, la met en application pour rendre beau l’utile et le nécessaire, et attirant ce qui ne pourrait être que superflu.

Si soudain, votre regard se pose, s’accroche, et qu’une sensation naît en vous, comme un sentiment inexplicable vous laissant perplexe face à beauté immatérielle, peut-être êtes vous en présence d’une réalisation utilisant le rapport divin.
Il est évident que, armé d’un compas de proportion, et d’une  l’obstination à toute épreuve, la toile d’un peintre, la sculpture d’un artiste, ou un monument nous livrera des secrets que même son auteur ignorait.

Mais comment faire la différence :

            La divine proportion inspire-t-elle la beauté ?

            Ou bien la beauté n’est-t-elle que divines proportions ?

R\ R\

7033-4 L'EDIFICE  -  contact@ledifice.net \